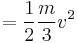Effective mass (spring-mass system)
In a spring-mass system the mass of the spring  , as well as the suspended mass
, as well as the suspended mass  , have an influence on the motion. However, since not all of the spring moves at the same velocity as the suspended mass, the mass of the spring cannot be simply added to the suspended mass. The effective mass of the spring is the mass which must be added to the suspended mass to correctly predict the behavior of the system.
, have an influence on the motion. However, since not all of the spring moves at the same velocity as the suspended mass, the mass of the spring cannot be simply added to the suspended mass. The effective mass of the spring is the mass which must be added to the suspended mass to correctly predict the behavior of the system.
Contents |
Ideal spring
The effective mass of the spring in a spring-mass system when using an ideal spring is independent whether the direction of the spring-mass system is horizontal, vertical or oblique, is also 1/3 of the mass of the spring, i.e., m/3. This can be shown by integration:
Its length is 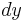 , mass is
, mass is 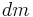 , velocity is
, velocity is  and so
and so
where  is the length of the spring.
is the length of the spring.
Hence the total kinetic energy of the spring and mass is
But the velocity of each position of the spring is directly proportional to its length and so
Hence
With comparison of the original kinetic energy formula 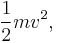 we can conclude that effective mass of spring in this case is m/3, i.e., 1/3 of the mass of the spring.
we can conclude that effective mass of spring in this case is m/3, i.e., 1/3 of the mass of the spring.
Real spring
However, the above calculations are only suitable for small values of 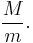 Since Jun-ichi Ueda and Yoshiro Sadamoto have done the experiment. It is found that, as the ratio
Since Jun-ichi Ueda and Yoshiro Sadamoto have done the experiment. It is found that, as the ratio 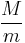 increases beyond 7, the effective mass of a spring in a vertical spring-mass system becomes smaller than Rayleigh's value
increases beyond 7, the effective mass of a spring in a vertical spring-mass system becomes smaller than Rayleigh's value 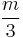 and eventually reaches negative values. This unexpected behavior of the effective mass can be explainable in terms of the elastic after-effect.
and eventually reaches negative values. This unexpected behavior of the effective mass can be explainable in terms of the elastic after-effect.
See also
External links
- http://tw.knowledge.yahoo.com/question/question?qid=1405121418180
- http://tw.knowledge.yahoo.com/question/question?qid=1509031308350
- http://hk.knowledge.yahoo.com/question/article?qid=6908120700201
- http://www.goiit.com/posts/list/mechanics-effective-mass-of-spring-40942.htm
- http://www.juen.ac.jp/scien/sadamoto_base/spring.html
- "The Effective Mass of an Oscillating Spring" Amer. J. Phys., 38, 98 (1970)
- "Effective Mass of an Oscillating Spring" The Physics Teacher, 45, 100 (2007)
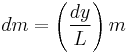
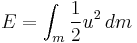
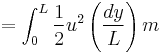
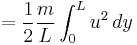
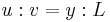
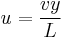
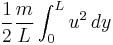
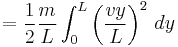
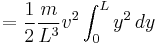
![=\frac{1}{2}\frac{m}{L^3}v^2\left[\frac{y^3}{3}\right]_0^L](/2012-wikipedia_en_all_nopic_01_2012/I/7e0d17314a72b0daa626c5a8dc936ccc.png)